Refinement Model

Overview

The RefinementModel coordinates adaptive mesh refinement (h-refinement) within a simulation. It registers geometric and topological coefficient functions useful for visualization, reporting, and refinement criteria. It also interacts with other models that implement refinement logic by querying them before modifying the mesh.

Functions

class RefinementModel

The RefinementModel provides mesh refinement capabilities in the simulation.

refine_mesh()

Refines the mesh based on refinement suggestions from other models.

All models that implement the refinement interface are queried to mark which cells should be refined. The marked cells are then refined in parallel using MFEM’s nonconforming mesh support.

Returns: None

uniform_refinement()

Performs uniform refinement of the entire mesh.

This subdivides all cells uniformly without checking any refinement criteria. Useful for debugging, convergence studies, or testing.

Returns: None

Coefficient Functions

Following functions are available for the refinement model for visualization or querying:

List of functions

Name	Example	Description
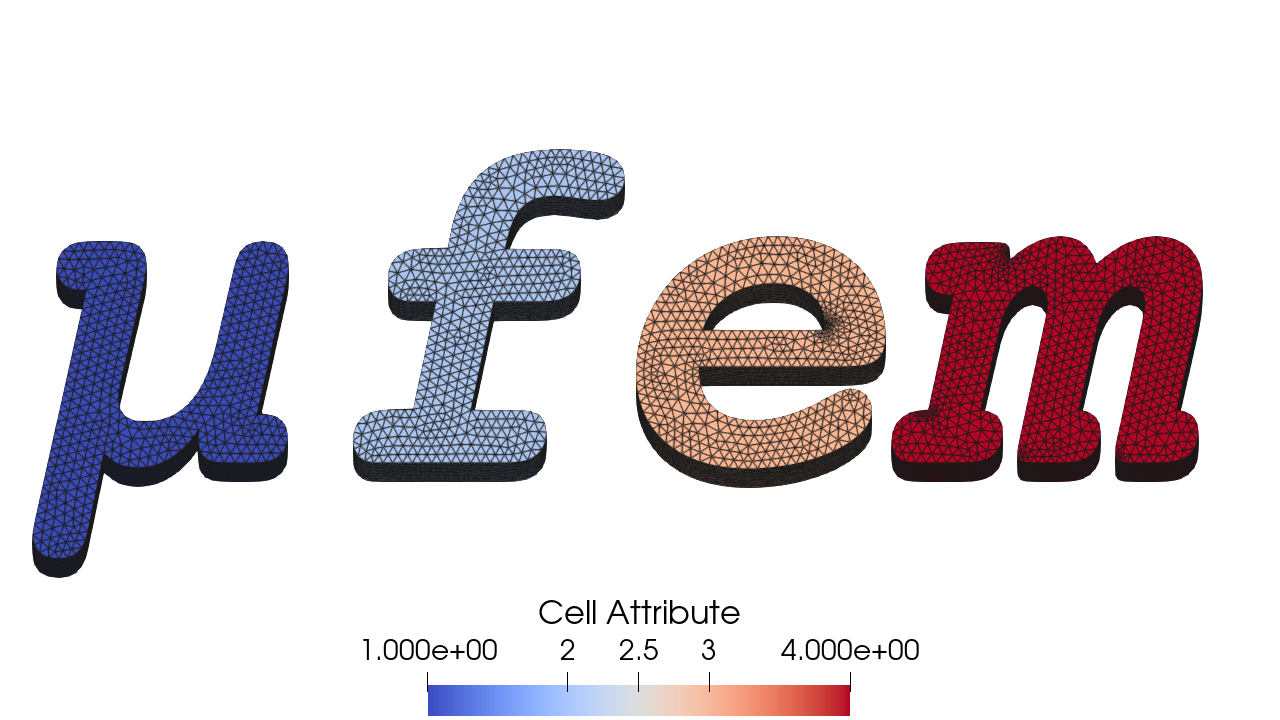
Cell Attribute [-] (Scalar Field)		The Cell Attribute provides the attribute of each cell in the mesh. It is used to identify different regions of the mesh, relevant for conditions and materials.
Cell Volume [m^3] (Scalar Field)		The Cell Volume provides the volume of each cell in the mesh.
Cell Aspect Ratio [-]		The Cell Aspect Ratio provides the aspect ratio of each cell in the mesh. It is given by the ratio of the smallest and largest eigenvalue of the Jacobian: \[r = \frac{\lambda_{\text{max}}}{\lambda_{\text{min}}} \quad,\] where \(\lambda_{\text{min}}\) and \(\lambda_{\text{max}}\) are the smallest and largest eigenvalues of the Jacobian matrix of the cell. Generally, a value close to 1 indicates a well-shaped cell, while larger values indicate distorted cells. Values above 10 are considered poor quality.
Element Type [-]		The Element Type provides the type of each element in the mesh, e.g., tetrahedron, hexahedron, prism.
Position [m]	Vector Field	The Position provides the physical coordinates of the center of each cell.
Refinement Level [-]		The Refinement Level provides the current refinement depth of each cell. It is incremented each time a cell is refined.
Global Cell Index [-]		The Global Cell Index is a globally unique identifier for each cell. It is stable across processes and refinements. Note that this should only be used for debugging purposes. Also note that that this index can change after refinement.
Local Cell Index [-]		The Local Cell Index is a globally unique identifier for each cell. It is stable across processes and refinements. Note that this should only be used for debugging purposes. Also note that that this index can change after refinement.

Example

In this example, we load a mesh, perform uniform refinement, and visualize the coefficient functions using the Field Exporter and ParaView.

import mufem

sim = mufem.Simulation.New("My Case", f"data/geometry.mesh", print_only_warnings=True)

refinement_model = mufem.RefinementModel()

sim.get_model_manager().add_model(refinement_model)

refinement_model.uniform_refinement()

field_exporter = sim.get_field_exporter()

field_exporter.add_field_output("Cell Volume")
field_exporter.add_field_output("Element Type")
field_exporter.add_field_output("Position")
field_exporter.add_field_output("Refinement Level")
field_exporter.add_field_output("Global Cell Index")

field_exporter.save()