Time-Domain Magnetic Model¶

Introduction¶

This model uses the quasi-static approximation of Maxwell's equations where wave and displacement effects are neglected. This model is usually used to model low-frequency applications, where magnetic fields and eddy currents are dominating, such as in electric machines, transformers, and induction heating.

The model here uses the so-called A-formulation (also known as electric formulation), where we are solving for the magnetic vector potential $\mathbf{A}$, given by:

\[ \begin{align} \operatorname{curl} \nu \operatorname{curl} \mathbf{A} + \sigma \frac{\partial \mathbf{A}}{\partial t} = \mathbf{J} + \nu \operatorname{curl} \mathbf{B}_r\, , \end{align} \]

where:

$\nu$ is the symmetric rank-2 reluctivity tensor,
$\sigma$ is the symmetric rank-2 electrical conductivity tensor,
$\mathbf{J}$ is a prescribed divergence-free current density ($\operatorname{div} \mathbf{J}= 0$),
$\mathbf{B}_r$ is the remanent flux density.

Note that the magnetic flux density is related to the magnetic vector potential by:

\[ \begin{align} \mathbf{B} = \operatorname{curl} \mathbf{A}, \end{align} \]

The magnetic reluctivity is the inverse of the magnetic permeability tensor ($\nu = \mu^{-1}$). The electric conductivity tensor $\sigma$ is usually a diagonal tensor, where the off-diagonal terms are zero. It describes how well a material conducts electric current. The remanent flux density is related to the remanent magnetization ($\mathbf{M}_r$) by $\mathbf{B}_r = \mu \mathbf{M}_r$.

Equation (1) is augmented by the constitutive equations:

\[ \begin{align} \mathbf{H} &= \nu \left( \mathbf{B} - \mathbf{B}_r \right), \\ \mathbf{J} &= \sigma \mathbf{E}, \end{align} \]

Note that in general the material properties: $\nu$, $\sigma$, and $\mathbf{M}$ can be nonlinear and dependent on other physical properties such as temperature.

In Eq. (1), the prescribed current density $\mathbf{J}$ on the right-hand side is set through support models such as the Excitation Coil Model.

Model¶

The model can be created and added to the simulation using

time_domain_magnetic_model = TimeDomainMagneticModel(
    marker=["Air", "Cylinder"] @ Vol,
    order=1,
    magnetostatic_initialization=True
)

sim.get_model_manager().add_model(time_domain_magnetic_model)

where - marker determines where the domain on which the model is solved - order the model order - magnetostatic_initialization wether an initial condition is obtained from solver the magnetostatic solution first

Materials¶

The model given by Eq. (1) requires the provision of material properties, specifically the magnetic reluctivity (inverse permeability), the electrical conductivity and the magnetization. A material is created by specifying methods to compute each of those three material properties. Most materials can be setup using the General Material with an example provided in Table 1.

Table 1: General Material Example
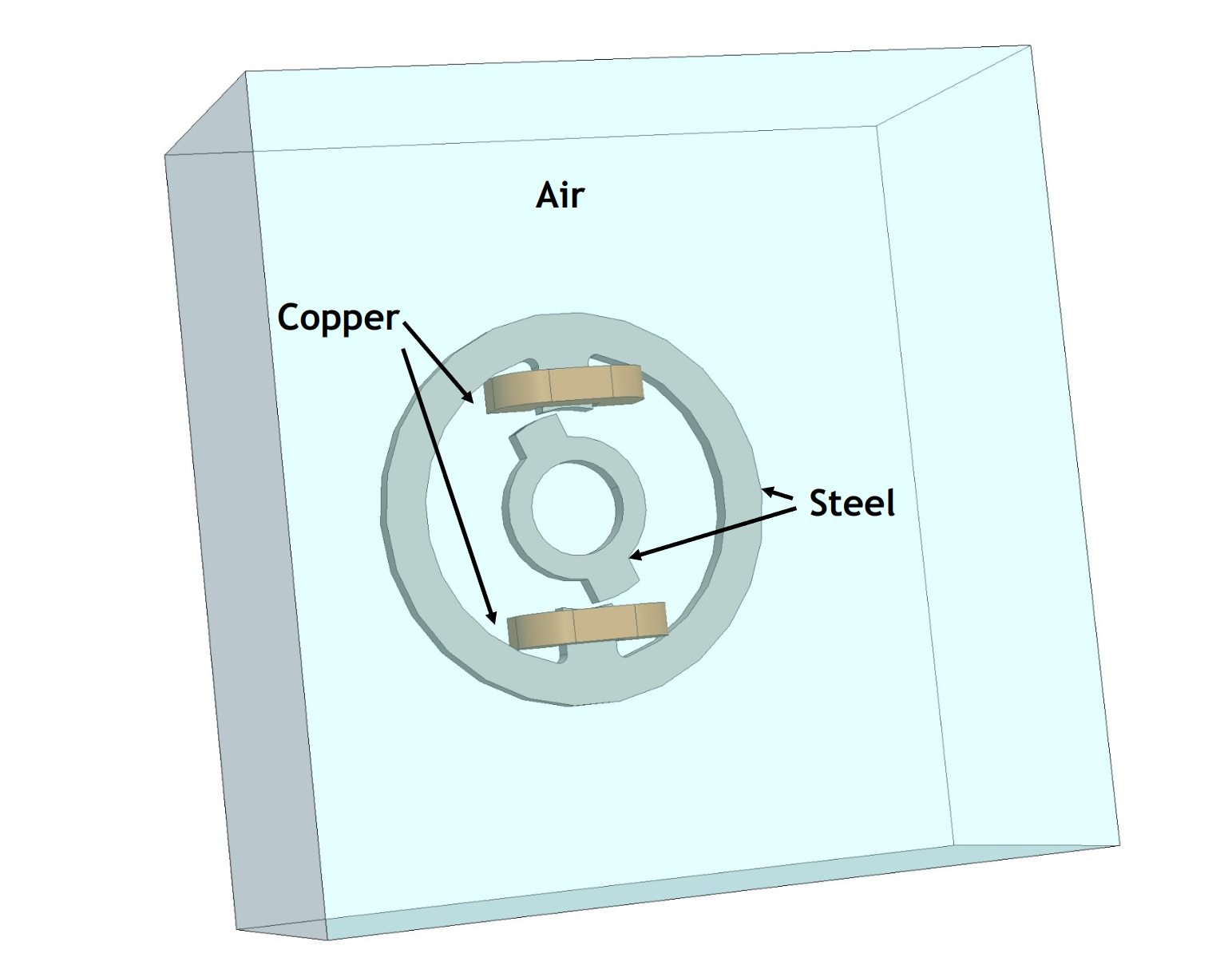Example simulation with three materials: Air, Copper and Steel.	Air For non-magnetic and non-conductive regions such as air with $$ \mu = \mu_0,\qquad \sigma = 0,\qquad \mathbf{B}_r = 0 $$ we can create the material using: `air_material = TimeDomainMagneticGeneralMaterial( name="Air", marker="Air" @ Vol )` Copper For non-magnetic but electrically conductive regions such as copper with $$ \mu = \mu_0,\qquad \sigma = \sigma_{\text{Cu}},\qquad \mathbf{B}_r = 0 $$ we can create the material using: `copper_material = TimeDomainMagneticGeneralMaterial( name="Copper", marker=["Upper Coil", "Lower Coil"] @ Vol, electric_conductivity=5.8e7, has_eddy_currents=False, )` Steel For magnetic and electrically conductive regions such as steel with $$ \mu = \mu(\|\mathbf{B}\|),\qquad \sigma = \sigma_{\text{steel}},\qquad \mathbf{B}_r = 0 $$ we can create the material using: `steel_material = TimeDomainMagneticGeneralMaterial( name="Steel", marker=["Rotor", "Stator"] @ Vol, magnetic_permeability=([0, 1000, 2000, ...], [0.0, 0.7, 1.0, ...]), electric_conductivity=4.5e6, )`

Note that once created the materials need to be added to the model

time_domain_magnetic_model.add_materials([air_material, copper_material, steel_material])

More complex materials like hysteric, laminated and superconducting materials are supported in their respective modules.

Conditions¶

Following conditions are available for the time-domain magnetic model:

List of supported conditions
Name	Supported Entities	Description
Tangential Magnetic Flux	Boundary	As boundary conditions, we support the tangential magnetic flux given by: $$ \mathbf{n} \cdot \mathbf{B} = 0 $$ on the boundary $\Gamma_0$.
Normal Magnetic Field	Boundary	The normal magnetic field given by: $$ \left. \mathbf{H} \times \mathbf{n} \right\|_{\Gamma_0} = 0. $$
Tangential Magnetic Field	Boundary	The tangential magnetic field given by $$ \left. \mathbf{H} \times \mathbf{n} \right\|_{\Gamma_0} = \mathbf{H}_\text{usr}, $$ where $\mathbf{H}_\text{usr}$ is the user-defined external magnetic field imposed on the boundary $\Gamma_0$.

Reports¶

Following reports are available for the time-domain magnetic model for visualization:

List of reports
Name	Field Type	Description
Magnetic Force Report	Scalar	Returns the magnetic force density on an object
Magnetic Torque Report	Scalar	Returns the magnetic force density on an object

Coefficients¶

Following functions are available for the time-domain magnetic model for visualization or querying:

List of functions
Name	Field Type	Description
Magnetic Flux Density	Vector	The magnetic flux density is computed as: $$ \mathbf{B} = \mathbf{\nabla} \times \mathbf{A}. $$
Magnetic Field	Vector	The magnetic field is given by: $$ \mathbf{H} = \bar{\bar{\nu}} \mathbf{B} - \mathbf{H}_c, $$ where $\mathbf{H}_c$ is the coercive force.
Electric Current Density	Vector	The electric current density inside the simulation domain which is the sum of the the eddy current density and the current density from the coils.
Ohmic Heating	Scalar	The ohmic heating is computed as: $$ P_\Omega = \mathbf{J} \cdot \mathbf{E}. $$
Electric Conductivity	Symmetric Tensor	The tensor of electric conductivity $\bar{\bar{\sigma}}$