Skip to content

Time-Harmonic Magnetic Model

Introduction

The time-harmonic magnetic model describes electromagnetic fields in terms of their complex amplitudes at a single angular frequency \(\omega = 2\pi f\), under the low-frequency (eddy-current) approximation where displacement currents are neglected. This approximation is applicable when wave-propagation effects are negligible compared to diffusion/induction effects, which is typical for many low-frequency magnetic devices.

The time-harmonic magnetic model solves $$ \nabla \times \left( \nu \nabla \times \tilde{\mathbf{A}} \right) + j \omega \sigma \tilde{\mathbf{A}} = \tilde{\mathbf{J}}_\mathrm{s}, $$

where * \(\nu = 1/\mu\) is the magnetic reluctivity * \(\sigma\) is the electric conductivity * \(\tilde{\mathbf{J}}_\mathrm{s}\) is the impressed (source) current density.

In a conductive material, the induced (eddy) current density is given by \(\tilde{\mathbf{J}} = \sigma \tilde{\mathbf{E}}\).

Model

The model can be created and added to the simulation using 

time_harmonic_magnetic_model = TimeHarmonicMagneticModel(
    marker=magnetic_domain,
    frequency=60, 
    order=2
)

sim.get_model_manager().add_model(time_harmonic_magnetic_model)
where - marker specifies the domain on which the model is solved - frequency \(\left[ \mathrm{Hz} \right]\) is the frequency of the fields - order is the polynomial order of the discretization

Materials

In the most general case, the material parameters \(\nu\) and \(\sigma\) in the equation above can be complex, frequency-dependent tensors that vary spatially and may also depend on other physical properties, such as temperature. A material is specified through the Time-Harmonic General Magnetic Material. For details refer to Time-Harmonic General Magnetic Material.

Most materials can be set up using the General Material, with an example provided in Table 1.

Table 1: General Material Example
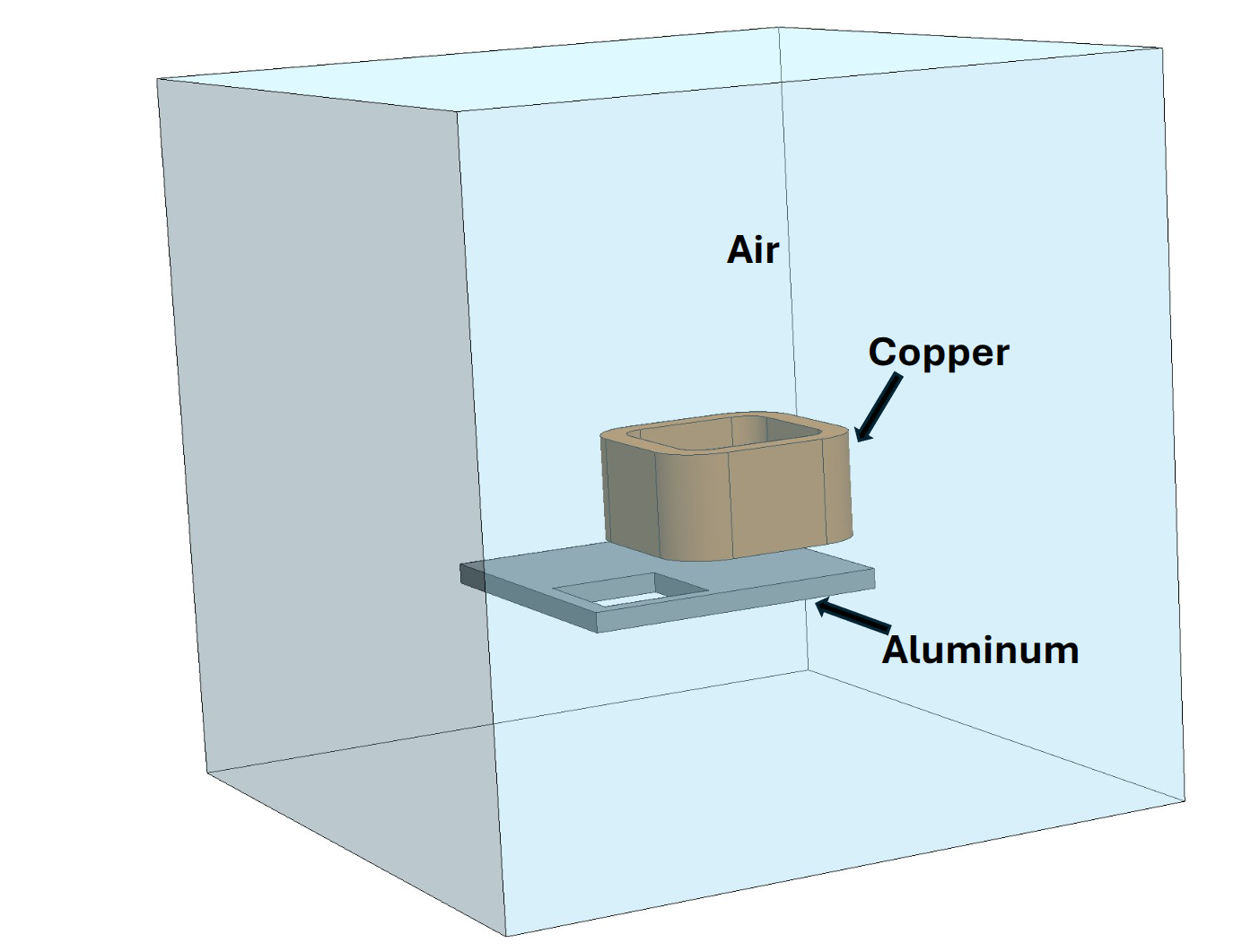materials
Example from the Compumag TEAM-7 case. The simulation contains three materials: Air, Copper and Aluminum. 		Air
For non-magnetic and non-conductive regions such as air with $$ \mu = \mu_0, \qquad \sigma = 0, $$ we can create the material using: 
air_material = TimeHarmonicMagneticGeneralMaterial(
    name="Air",
    marker="Air" @ Vol
)
Copper
For non-magnetic but electrically conductive regions such as copper with $$ \mu = \mu_0, \qquad \sigma = \sigma_{\text{Cu}}, $$ we can create the material using: 
copper_material = TimeHarmonicMagneticGeneralMaterial(
    name="Copper",
    marker=["Upper Coil", "Lower Coil"] @ Vol,
    electric_conductivity=5.8e7,
    has_eddy_currents=False,
)
(eddy currents are neglected here because the coil is stranded). Aluminum
For electrically conductive regions such as aluminum we use $$ \mu = \mu_0, \qquad \sigma = \sigma_{\text{Al}}, $$ we can create the material using: 
aluminum_material = TimeHarmonicMagneticGeneralMaterial(
    name="Aluminum",
    marker=["Rotor", "Stator"] @ Vol,
    magnetic_permeability=1.0,
    electric_conductivity=4.5e6,
    has_eddy_currents=True,
)

Note that, once created, the materials need to be added to the model: 

time_harmonic_magnetic_model.add_materials([air_material, copper_material, aluminum_material])

Conditions

The governing equation is solved within a specific domain and must be accompanied by appropriate boundary conditions and excitations.

List of supported conditions
Name Supported Entities Description
Tangential Magnetic Flux Boundary Enforces the magnetic flux density to be tangential to the boundary.
Normal Magnetic Field Boundary Enforces the magnetic field to be normal to the boundary.
Tangential Magnetic Field Boundary Sets the tangential component of the magnetic field on the boundary.

Reports

Coefficients

The following functions are available in the time-harmonic magnetic model for visualization or querying:

List of functions
Name Field Type Description
Magnetic Vector Potential-Real Vector The real part of the complex amplitude of magnetic vector potential: $$ \mathrm{Re}\left\{\tilde{\mathbf{A}}\right\} $$
Magnetic Vector Potential-Imag Vector The imaginary part of the complex amplitude of magnetic vector potential: $$ \mathrm{Im}\left\{\tilde{\mathbf{A}}\right\} $$
Magnetic Flux Density-Real Vector The real part of the complex amplitude of magnetic flux density: $$ \mathrm{Re}\left\{\tilde{\mathbf{B}}\right\} = \mathrm{Re}\left\{\nabla \times \tilde{\mathbf{A}}\right\} $$
Magnetic Flux Density-Imag Vector The imaginary part of the complex amplitude of magnetic flux density: $$ \mathrm{Im}\left\{\tilde{\mathbf{B}}\right\} = \mathrm{Im}\left\{\nabla \times \tilde{\mathbf{A}}\right\} $$
Magnetic Field-Real Vector The real part of the magnetic field vector, calculated as $$ \mathrm{Re}\left\{\tilde{\mathbf{H}}\right\} = \mathrm{Re}\left\{\nu \, \tilde{\mathbf{B}}\right\}, $$ where $\nu$ is the magnetic reluctivity and $\tilde{\mathbf{B}}$ is the magnetic flux density vector.
Magnetic Field-Imag Vector The imaginary part of the magnetic field vector, calculated as $$ \mathrm{Im}\left\{\tilde{\mathbf{H}}\right\} = \mathrm{Im}\left\{\nu \, \tilde{\mathbf{B}}\right\}, $$ where $\nu$ is the magnetic reluctivity and $\tilde{\mathbf{B}}$ is the magnetic flux density vector.
Electric Current Density-Real Vector The real part of the electric current density: $$ \mathrm{Re}\left\{\tilde{\mathbf{J}}\right\} = -\omega \, \mathrm{Re}\left\{j \sigma \tilde{\mathbf{A}}\right\}, $$ where $\omega$ is the angular frequency, $\sigma$ is the electric conductivity, and $\tilde{\mathbf{A}}$ is the magnetic vector potential.
Electric Current Density-Imag Vector The imaginary part of the electric current density: $$ \mathrm{Im}\left\{\tilde{\mathbf{J}}\right\} = -\omega \, \mathrm{Im}\left\{j \sigma \tilde{\mathbf{A}}\right\}, $$ where $\omega$ is the angular frequency, $\sigma$ is the electric conductivity, and $\tilde{\mathbf{A}}$ is the magnetic vector potential.
Ohmic Heating Scalar Time-averaged ohmic loss density: $$ P_\Omega = \frac{1}{2} \mathrm{Re}\left\{ \tilde{\mathbf{J}} \cdot \tilde{\mathbf{E}}^* \right\}, $$ where $^*$ denotes the complex conjugate.
Magnetic Permeability Scalar The magnetic permeability is the inverse of the magnetic reluctivity: $\mu = 1/\nu$.